Πώς να βρείτε μια διαγώνιο με διαμάντια;

Ένας ρόμβος είναι μια γεωμετρική μορφή που αποτελείται απόίσες και παράλληλες μεταξύ τους τέσσερις πλευρές. Για να πάρετε μια διαγώνιο ενός ρομπότ, πρέπει να συνδέσετε τις αντίθετες κορυφές ενός δεδομένου γεωμετρικού σχήματος. Οι διαγωνίσεις του τέμνονται σε μια ορθή γωνία, δημιουργώντας έτσι τέσσερα ορθογώνια τρίγωνα στη μέση του ρομβοειδούς.

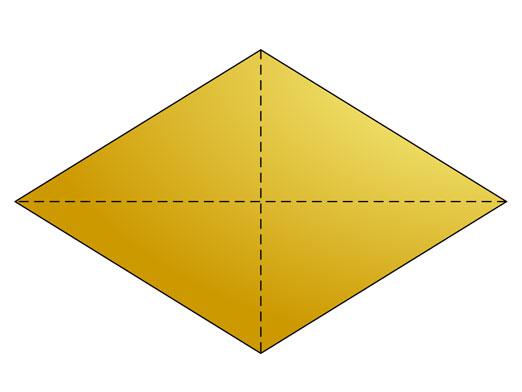
Γραφικό στοιχείο της εργασίας

Για να καταλάβουμε πώς να βρούμε τη διαγώνια ενός ρομπότ,πρώτα από όλα είναι απαραίτητο να παρουσιάσει το γραφικό του σχέδιο. Επίσης, για λόγους σαφήνειας, πρέπει να ονομάσετε τις κορυφές του διαμαντιού με τα γράμματα Α, Β, Γ και Δ, το σημείο τομής των διαγωνίων είναι το γράμμα Ο, θα είναι το κέντρο του διαμαντιού.

Οι γωνίες DAB και DΣΒ είναι ίσες μεταξύ τους, επομένως για λόγους ευκολίας μπορούν να αναφέρονται ως α. a είναι το μήκος της άκρης του ρόμβου.

Υπολογίστε τη μικρή διαγώνιο του ρομβοειδούς

Πρώτον, είναι καλύτερα να βρείτε το μήκος της μικρότερης διαγώνιας του διαμαντιού. Το τρίγωνο COD είναι ορθογώνιο. Αυτό σημαίνει ότι μια γωνία είναι 90 °, και το ίδιο το τρίγωνο αποτελείται από δύο πόδια και μια υποτείνουσα. CO και OD είναι τα πόδια του τριγώνου, το CD είναι η υποτείνουσα, η γωνία DOC είναι 90 °.

Η διαγώνια του ρομβοειδούς είναι ίση με τη διχοτόμηση των γωνιών της, από την οποία προκύπτει ότι η γωνία OCD = α / 2.

Ακολουθήστε τον τύπο OD = 1 / 2BD = CD * sin (α / 2). Μπορούμε να συμπεράνουμε ότι BD = 2a * sin (α / 2).

Υπολογίστε τη μεγάλη διαγώνιο του ρόμβου

Για να βρείτε μια μεγάλη διαγώνιο με διαμάντια, είναι απαραίτητο να εκτελέσετε παρόμοιες ενέργειες και να λάβετε υπόψη ότι ο τύπος είναι ελαφρώς διαφορετικός: OS = AC * (1/2) = CD * cos (α / 2).

Επομένως, το μήκος ολόκληρης της διαγώνιας θα είναι: AC = 2a * cos (α / 2).

Πλατεία Diamond

Γνωρίζοντας το μήκος των διαγώνων του διαμαντιού, είναι πολύ εύκολο να βρείτε την περιοχή του. Τις περισσότερες φορές, το μήκος των διαγωνίων υπολογίζεται για αυτό.

Η περιοχή του διαμαντιού υποδηλώνεται υπό όρους με το γράμμα S. Τύπος περιοχής: S = (AC * BD) / 2.

Στο και βρήκε την επιθυμητή τιμή - τη διαγώνιο του ρομβοειδούς, και επιπλέον, επίσης, την περιοχή αυτής της γεωμετρικής μορφής.