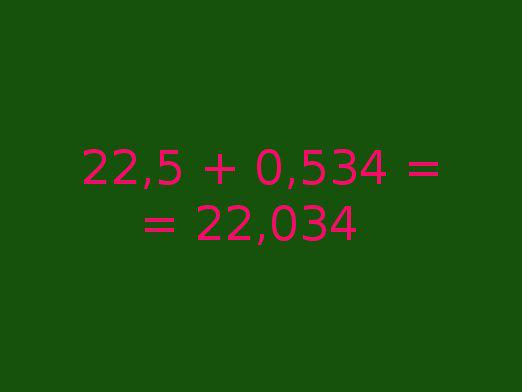Πώς να οδηγήσετε σε έναν κοινό παρονομαστή;
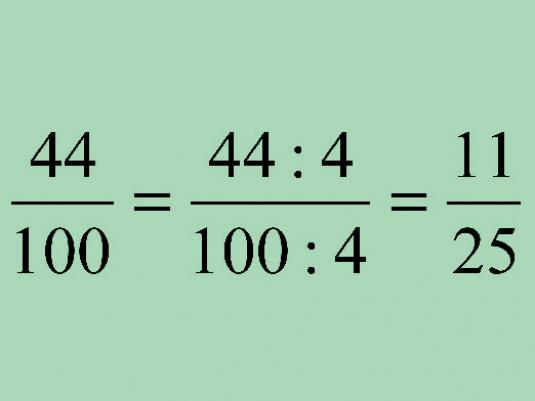
Για να προσθέσετε ή να αφαιρέσετε κλάσματα,πρώτα πρέπει να οδηγηθούν σε έναν κοινό παρονομαστή. Πώς να το κάνετε αυτό; Για να βρείτε τον μικρότερο κοινό παρονομαστή για κλάσματα, πρέπει να εκτελέσετε τα παρακάτω βήματα.
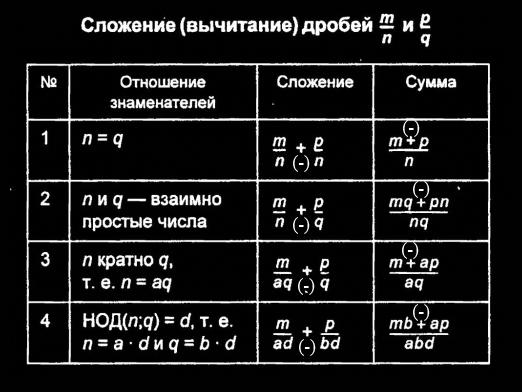
Σχέδιο μείωσης στον κοινό παρονομαστή
- Είναι απαραίτητο να καθοριστεί ποιο θα είναι το λιγότερο κοινόφορές για τους παρονομαστές των κλασμάτων. Εάν πρόκειται για ένα μεικτό ή έναν ακέραιο, τότε πρέπει πρώτα να μετατραπεί σε κλάσμα, και μόνο τότε να καθορίσει το μικρότερο κοινό πολλαπλάσιο. Για να μετατρέψουμε έναν ακέραιο σε κλάσμα, είναι απαραίτητο να γράψουμε αυτόν τον αριθμό στον αριθμητή και στον παρονομαστή είναι απαραίτητο να γράψουμε ένα. Για παράδειγμα, ο αριθμός 5 με τη μορφή ενός κλάσματος θα μοιάζει με αυτό: 5/1. Για να μετατρέψετε ένα μικτό αριθμό σε κλάσμα, πολλαπλασιάστε τον αριθμό με τον παρονομαστή και προσθέστε τον αριθμητή σε αυτόν. Παράδειγμα: 8 ακέραιοι αριθμοί και 3/5 με τη μορφή των κλασμάτων = 8x5 + 3/5 = 43/5.
- Μετά από αυτό, είναι απαραίτητο να βρεθεί ένας επιπλέον παράγοντας, ο οποίος προσδιορίζεται διαιρώντας τα NOx από τον παρονομαστή κάθε κλάσματος.
- Το τελευταίο βήμα είναι να πολλαπλασιάσουμε το κλάσμα με έναν πρόσθετο παράγοντα.
Είναι σημαντικό να θυμάστε ότι φέρνοντας στο γενικόΟ παρονομαστής χρειάζεται όχι μόνο για προσθήκη ή αφαίρεση. Για να συγκρίνουμε διάφορα κλάσματα με διαφορετικούς παρονομαστές, είναι επίσης απαραίτητο να φέρνουμε πρώτα καθένα από αυτά σε έναν κοινό παρονομαστή.
Δώστε κλάσματα στον κοινό παρονομαστή
Για να κατανοήσουμε πώς να οδηγήσουμε σε μια κοινήτα κλάσματα παρανομαστή, είναι απαραίτητο να κατανοήσουμε κάποιες από τις ιδιότητες των κλασμάτων. Έτσι, μια σημαντική ιδιότητα που χρησιμοποιείται για να φέρει στο NOZ είναι η ισότητα των κλασμάτων. Με άλλα λόγια, αν ο αριθμητής και ο παρονομαστής του κλάσματος πολλαπλασιάζονται με έναν αριθμό, το αποτέλεσμα είναι ένα κλάσμα ίσο με το προηγούμενο. Για παράδειγμα, δίνουμε το ακόλουθο παράδειγμα. Για να φέρετε τα κλάσματα 5/9 και 5/6 στον μικρότερο κοινό παρονομαστή, πρέπει να κάνετε τα εξής:
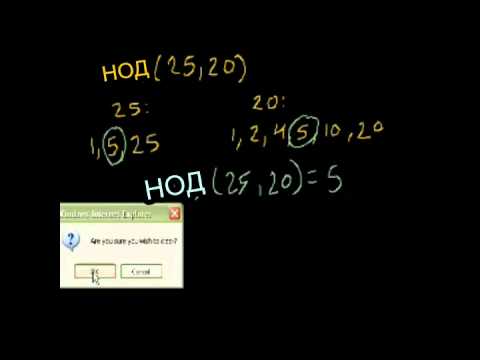
- Πρώτον, βρίσκουμε το μικρότερο κοινό πολλαπλάσιο των παρονομαστών. Στην περίπτωση αυτή, για τους αριθμούς 9 και 6, το NOC θα είναι ίσο με 18.
- Προσδιορίζουμε τους πρόσθετους παράγοντες για κάθε ένα από τακλάσματα. Αυτό γίνεται ως εξής. Διαχωρίζουμε το LCM από τον παρονομαστή καθενός από τα κλάσματα, με αποτέλεσμα να έχουμε 18: 9 = 2, και 18: 6 = 3. Αυτοί οι αριθμοί θα είναι πρόσθετοι παράγοντες.
- Δίνουμε δύο κλάσματα στο NOZ. Πολλαπλασιάζοντας ένα κλάσμα από έναν αριθμό, πολλαπλασιάστε τον αριθμητή και παρονομαστή. Κλάσμα 09/05 μπορεί να πολλαπλασιάζεται με ένα πρόσθετο παράγοντα 2, με αποτέλεσμα το κλάσμα που λαμβάνεται, ίση με ένα δεδομένο - 10/18. Το ίδιο γίνεται με τη δεύτερη βολή: 5/6 πολλαπλασιάζεται με 3, με αποτέλεσμα να έχουμε 15/18.
Όπως μπορούμε να δούμε από το παραπάνω παράδειγμα, και τα δύοΤα κλάσματα μειώθηκαν στον χαμηλότερο κοινό παρονομαστή. Για να καταλάβουμε τελικά πώς να βρούμε έναν κοινό παρονομαστή, θα πρέπει να καταλάβετε μια ακόμα ιδιότητα των κλασμάτων. Συνίσταται στο γεγονός ότι ο αριθμητής και ο παρονομαστής ενός κλάσματος μπορούν να μειωθούν με τον ίδιο αριθμό, ο οποίος καλείται κοινός διαιρέτης. Για παράδειγμα, ένα κλάσμα 12/30 μπορεί να μειωθεί σε 2/5 αν διαιρείται με κοινό διαιρέτη - τον αριθμό 6.