Πώς να λύσετε ανισότητες;
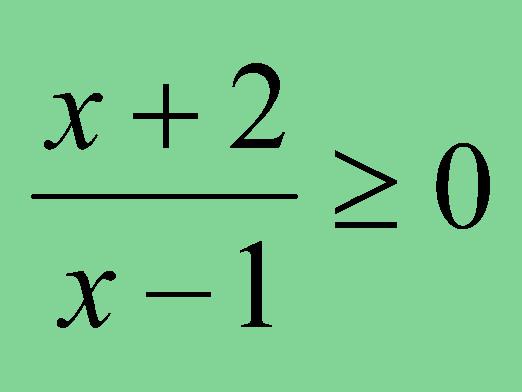
Όλοι δεν ξέρουν πώς να λύσουν τις ανισότητεςη δομή τους έχει παρόμοια και διακριτικά χαρακτηριστικά με τις εξισώσεις. Η εξίσωση είναι μια άσκηση που αποτελείται από δύο μέρη, μεταξύ των οποίων υπάρχει ένα ισότιμο σημάδι, και μεταξύ των τμημάτων της ανισότητας μπορεί να υπάρχει ένα σημάδι "περισσότερο" ή "λιγότερο". Έτσι, πριν βρούμε μια λύση σε μια συγκεκριμένη ανισότητα, πρέπει να καταλάβουμε ότι είναι απαραίτητο να ληφθεί υπόψη το σημάδι ενός αριθμού (θετικό ή αρνητικό) εάν είναι αναγκαίο να πολλαπλασιαστούν και τα δύο μέρη με μια έκφραση. Το ίδιο πρέπει να ληφθεί υπόψη εάν απαιτείται να τεθεί το επίκεντρο της επίλυσης της ανισότητας, διότι η τετραγωνισμός γίνεται με πολλαπλασιασμό.
Πώς να λύσετε το σύστημα των ανισοτήτων
Είναι πολύ πιο δύσκολο να επιλυθούν συστήματα ανισοτήτων απ 'ό, τισυνήθεις ανισότητες. Πώς να λύσουμε ανισότητες Βαθμός 9, να εξετάσει τα συγκεκριμένα παραδείγματα. Είναι κατανοητό ότι πριν από την επίλυση τετραγωνική ανισότητα (σύστημα) ή οποιοδήποτε άλλο σύστημα ανισοτήτων, είναι απαραίτητο για την επίλυση κάθε ανισότητα ξεχωριστά, και στη συνέχεια η σύγκρισή τους. λύση συστήματος ανισότητα θα είναι είτε θετική ή αρνητική απάντηση (ένα διάλυμα σύστημα ή ένα διάλυμα).
Ο στόχος είναι να επιλυθεί μια σειρά ανισοτήτων:
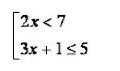
Αντιμετωπίζουμε κάθε ανισότητα ξεχωριστά

Κατασκευάζουμε μια αριθμητική γραμμή στην οποία αντιπροσωπεύουμε το σύνολο των λύσεων
Απάντηση:
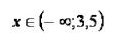
Δεδομένου ότι η συλλογή είναι μια ένωση από ομάδες λύσεων, αυτή η ρύθμιση στη γραμμή αριθμού πρέπει να υπογραμμιστεί από μία τουλάχιστον γραμμή.
Λύση ανισοτήτων με μια ενότητα
Αυτό το παράδειγμα θα δείξει πώς να λύσουμε τις ανισότητες με την ενότητα. Έτσι, έχουμε έναν ορισμό:

Πρέπει να λύσουμε την ανισότητα:
| x |> 2
Πριν από την επίλυση μιας τέτοιας ανισότητας, είναι απαραίτητο να απαλλαγούμε από την ενότητα (σημείο)
Ας γράψουμε, με βάση τον ορισμό:

ή

Τώρα είναι απαραίτητο να λύσουμε ξεχωριστά κάθε ένα από τα συστήματα.
Κατασκευάζουμε μια αριθμητική γραμμή στην οποία εκπροσωπούμε σύνολα λύσεων.
Ως αποτέλεσμα, έχουμε αποκτήσει ένα σύνολο που συνδυάζει πολλές λύσεις.
Απάντηση:

Λύση τετραγωνικών ανισοτήτων
Χρησιμοποιώντας την αριθμητική ευθεία, εξετάστε τη λύση των τετραγωνικών ανισοτήτων. Έχουμε ανισότητα:
Γνωρίζουμε ότι η γραφική παράσταση ενός τετραγωνικού τρινομίου είναι μια παραβολή. Γνωρίζουμε επίσης ότι οι κλάδοι μιας παραβολής κατευθύνονται προς τα πάνω, αν είναι> 0.
x2-3x-4 <0
Χρησιμοποιώντας το θεώρημα του Viet, βρίσκουμε τις ρίζες x1 = - 1. x2 = 4
Σχεδιάζουμε μια παραβολή ή μάλλον ένα σκίτσο.
Έτσι, διαπιστώσαμε ότι οι τιμές του τετραγωνικού τετραγώνου θα είναι μικρότερες από 0 στο τμήμα από το 1 έως το 4.
Απάντηση:

Πολλά ερωτήματα προκύπτουν κατά την επίλυση του διπλούανισότητες του τύπου g (x) <f (x) <q (x). Πριν λύσουμε τις διπλές ανισότητες, είναι απαραίτητο να τις αποσυνθέσουμε σε απλές και να λύσουμε ξεχωριστά κάθε απλή ανισότητα. Για παράδειγμα, επεκτείνοντας το παράδειγμά μας, έχουμε σαν αποτέλεσμα ένα σύστημα ανισοτήτων g (x) <f (x) και f (x) <q (x), το οποίο πρέπει να λυθεί.
Στην πραγματικότητα, υπάρχουν αρκετές μέθοδοι για την επίλυση ανισοτήτων, ώστε να μπορείτε να χρησιμοποιήσετε τη γραφική μέθοδο για να λύσετε πολύπλοκες ανισότητες.
Λύση των κλασματικών ανισοτήτων
Μια πληρέστερη προσέγγιση απαιτεί κλασματικήανισότητα. Αυτό οφείλεται στο γεγονός ότι στη διαδικασία επίλυσης ορισμένων κλασματικών ανισοτήτων το σημείο μπορεί να αλλάξει. Πριν από την επίλυση των κλασματικών ανισοτήτων, είναι απαραίτητο να γνωρίζουμε ότι η μέθοδος διαστήματος χρησιμοποιείται για την επίλυσή τους. Κλασματική ανισότητα πρέπει να υποβάλλονται με τέτοιο τρόπο ώστε η μία πλευρά του σημείου έμοιαζε με μια λογική έκφραση, και η δεύτερη - «- 0». Με τον μετασχηματισμό της ανισότητας με αυτόν τον τρόπο, έχουμε ως αποτέλεσμα f (x) / g (x)> (.
Επίλυση ανισοτήτων με τη μέθοδο διαστήματος
Η τεχνική διαστήματος βασίζεται στην πλήρηεπαγωγή, δηλαδή να βρούμε όλες τις πιθανές παραλλαγές για την εξεύρεση λύσης της ανισότητας. Αυτή η μέθοδος λύσης, ίσως, δεν θα είναι απαραίτητη για τους μαθητές της 8ης τάξης, αφού πρέπει να γνωρίζουν πώς να λύσουν τις ανισότητες της 8ης τάξης, οι οποίες είναι οι απλούστερες ασκήσεις. Αλλά για τις παλαιότερες κατηγορίες αυτή η μέθοδος είναι αναντικατάστατη, καθώς βοηθά στην επίλυση των κλασματικών ανισοτήτων. Η λύση των ανισοτήτων με τη βοήθεια αυτής της τεχνικής βασίζεται στην ιδιότητα μιας συνεχούς λειτουργίας, όπως η διατήρηση του σημείου μεταξύ των αξιών στις οποίες μετατρέπεται σε 0.
Κατασκευάζουμε το γράφημα του πολυωνύμου. Αυτή είναι μια συνεχής συνάρτηση που αποκτά μια τιμή 0 φορές, δηλαδή, το f (x) θα είναι 0 στα σημεία x1, χ2 και x3, τις ρίζες του πολυωνύμου. Μεταξύ αυτών των σημείων, το σημάδι της λειτουργίας διατηρείται.

Επειδή για την επίλυση της ανισότητας f (x)> 0 χρειαζόμαστε ένα σημάδι λειτουργίας, πηγαίνουμε στη γραμμή συντεταγμένων, αφήνοντας το γράφημα.

f (x)> 0 για το x (x1. x2) και για το x (x3. ),
f (x) x (-; x1) και για το x (x2. x3),
Το γράφημα δείχνει σαφώς τις λύσεις των ανισοτήτωνf (x) f (x)> 0 (μπλε για την πρώτη ανισότητα, και κόκκινο για το δεύτερο). Για να προσδιορίσετε Για να προσδιορίσετε το σημείο μιας λειτουργίας σε ένα διάστημα, αρκεί να γνωρίζετε το σημείο μιας λειτουργίας σε ένα από τα σημεία. Αυτή η τεχνική μας επιτρέπει να λύσουμε γρήγορα τις ανισότητες στις οποίες η αριστερή πλευρά παραγοντοποιείται, επειδή είναι αρκετά εύκολο να βρεθούν ρίζες σε τέτοιες ανισότητες.