Πώς να βρείτε την περιοχή ενός παραλληλεπίπεδου;

Στο γεωμετρικό σχήμα, ο παραλληλεπίπεδο έχειέξι πρόσωπα - τέσσερα βασικά και δύο βάσεις (εξ ορισμού είναι όλα τα παράλληλα γραφήματα). Εάν και οι έξι είναι ορθογώνια, τότε το παραλληλεπίπεδο θα είναι μια ευθεία γραμμή. Οι άκρες στις απέναντι πλευρές είναι ίσες και είναι παράλληλες. Οι τέσσερις διαγώνιες του παραλληλεπίπεδου συγκλίνουν σε ένα μόνο σημείο και διαιρούνται σε δύο.

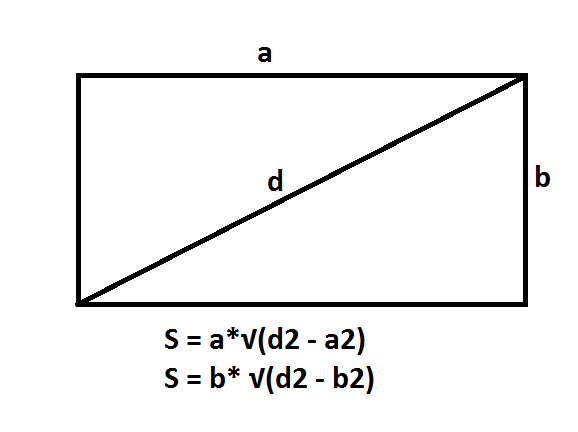
Για να μάθετε πώς μπορείτε να βρείτε μια περιοχήείναι απαραίτητο να υπολογιστεί πρώτα η περιοχή όλων των βάσεών της (που υποδηλώνεται με το γράμμα -α), την πλευρική της πλευρά (που υποδηλώνεται με το γράμμα -b), ενώ καθορίζεται το μήκος της βάσης και της ακμής.

Αρχικά, σχεδιάζουμε το ύψος του παραλληλογράμμου (που υποδηλώνεται με το γράμμα - h), κατόπιν με την άκρη του παραλληλεπίπεδου (που υποδηλώνεται με το γράμμα - H). Ή μέσα από τα μήκη των πλευρών (a, b, c).

Η συνολική επιφάνεια των βάσεων είναι: S = 2a * h ή S = 2ac

Δεδομένου ότι οι πλευρικές επιφάνειες είναι ορθογώνια, η περιοχή τους είναι: S = 2a * H και S = 2b * h ή S = 2a * b, S = 2b * c

Ως εκ τούτου, υπολογίσαμε πώς να βρούμε την περιοχήκυβοειδούς - τελικό τύπο υπολογισμού γράφεται ως: S = 2ah + 2Ah + 2bH = 2 (αχ + αΗ + bH) ή S = 2 (Sa + Sb + Sc) = 2 (ab + bc + ac), δηλαδή, δύο φορές το άθροισμα των περιοχών πρόσωπα παραλληλεπιπέδου.

Υπάρχουν περιπτώσεις όταν η πλευρά αντιμετωπίζειΤο παραλληλόγραμμο βρίσκεται σε οποιαδήποτε γωνία ως προς τη βάση του, τότε ο παραλληλεπίπεδο είναι κεκλιμένος. Στη συνέχεια υπολογίζεται η περιοχή των πλευρικών επιφανειών της, γνωρίζοντας το ύψος τους. Σε αυτή την περίπτωση, η επιφάνεια των βάσεων υπολογίζεται με τον ίδιο τρόπο.

Τίποτα περίπλοκο.