Πώς μπορώ να βρω το πλάτος ενός ορθογωνίου;

Η επίλυση προβλημάτων με τετράπλευρα είναι ένα από ταΤα πιο εκτεταμένα τμήματα της γεωμετρίας, τα οποία δίνουν στους μαθητές πολλές δυσκολίες. Σας προτείνουμε να ασχοληθείτε με τα τυπικά καθήκοντα στα οποία θέλετε να βρείτε το πλάτος ενός ορθογωνίου.

Πρώτα απ 'όλα, είναι απαραίτητο να θυμόμαστε τι είδουςκαι ποιες είναι οι κύριες ιδιότητές του. Ένα ορθογώνιο είναι τετράπλευρο με όλες τις γωνίες του ευθεία και τις αντίθετες πλευρές ίσες. Η οριζόντια πλευρά ονομάζεται πλάτος του ορθογωνίου και η κάθετη πλευρά ονομάζεται μήκος.

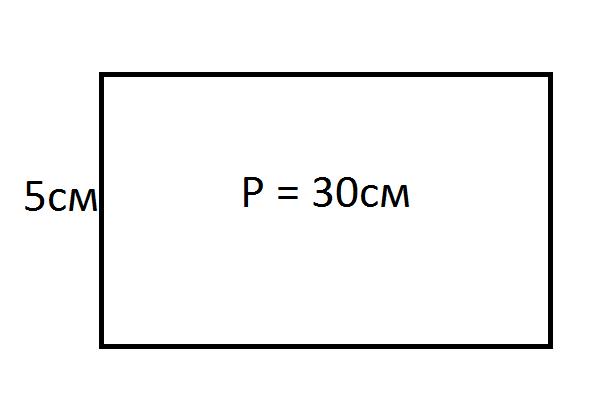
Πρόβλημα 1. Υπολογίστε το πλάτος, γνωρίζοντας την περίμετρο

Ας αναλύσουμε αυτό το είδος της εργασίας από το παράδειγμα της ακόλουθης εργασίας. Ορθογώνιο, περίμετρο

που είναι 36 cm και το μήκος είναι 16 cm. Είναι απαραίτητο να βρείτε το πλάτος. Η περίμετρος είναι το άθροισμα των πλευρών του σχήματος. Δεδομένου ότι οι αντίθετες πλευρές του ορθογωνίου είναι ίσες, ο τύπος της περιμέτρου του έχει την ακόλουθη μορφή: F = 2 (α + β), όπου α και b του ορθογωνίου.

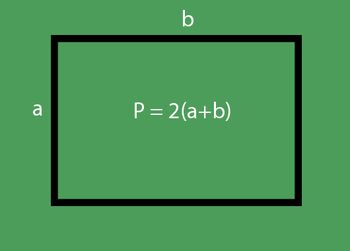
Παίρνουμε:

• b = Ρ: 2 - α = 36: 2-16 = 2 (cm)

Απάντηση: το πλάτος του ορθογωνίου είναι 2 cm.

Πρόβλημα 2. Βρείτε το πλάτος, γνωρίζοντας το μήκος και την περίμετρο

Ας περιπλέξουμε λίγο το έργο. Τώρα πρέπει να βρούμε το πλάτος του ορθογωνίου, αν είναι γνωστό ότι είναι 5 φορές μικρότερο από το μήκος του και η περίμετρος του τριγώνου είναι 120 cm.

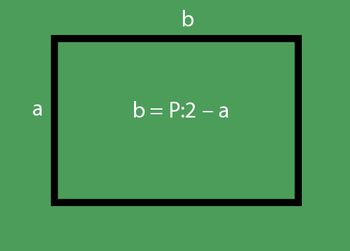
Από την κατάσταση του προβλήματος:

• α = 5b

Γνωρίζουμε ήδη ότι b = P: 2 - a. Αντικαθίστανται οι τιμές των P και a. Παίρνουμε:

• b = 120: 2-5b.
• 6b = 60;
• β = 60: 6
• b = 10 (cm).

Απάντηση: το πλάτος του ορθογωνίου είναι 10 εκατοστά.

Πρόβλημα 3. Προσδιορίστε το πλάτος εάν είναι γνωστή η περιοχή

Συνθήκη εργασίας: ο κήπος έχει ορθογώνιο σχήμα. Η έκτασή του είναι 400 000 τ.μ. και το μήκος είναι 400 μ. Ποιο είναι το πλάτος του κήπου;

Ένας κήπος λαχανικών είναι ένα ορθογώνιο. Η περιοχή ενός ορθογωνίου είναι ίση με το προϊόν των πλευρών του. Εάν γνωρίζουμε το μήκος και την περιοχή, το πλάτος θα είναι ίσο με:

• b = Ρ: α = 400.000: 400 = 1000 (m)

Απάντηση: Το πλάτος του κήπου είναι 1000 μ.

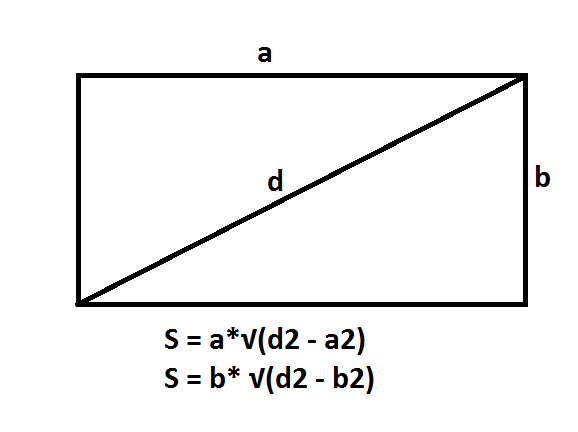
Πρόβλημα 4. Πώς να βρείτε το πλάτος, γνωρίζοντας τη διαγώνιο

Αυτό το έργο είναι ήδη λίγο πιο περίπλοκο από τα προηγούμενα. Σε αυτό, εκτός από τις ιδιότητες του ορθογωνίου, θα χρειαστεί να υπενθυμίσουμε τους τύπους ορθογώνιων τριγώνων. Ας υποθέσουμε ότι η διαγώνιος του AC του ορθογωνίου ABCD είναι 54,6 cm και η αναλογία μήκους-πλάτους είναι 16: 9. Είναι απαραίτητο να βρείτε το πλάτος του σχήματος.

Το τρίγωνο ABC έχει ορθή γωνία, που σημαίνει ότι είναι ορθογώνιο. Η διαγώνιος είναι η υποτείνουσα και οι πλευρές είναι τα πόδια.

Από την κατάσταση:

• 16AB = 9BC, επομένως AB = 9BC: 16

Από το θεώρημα του Πυθαγορείου:

• AC² = ΑΒ²+ Κυρ²

Αντικαθιστούμε τους αριθμούς:

• 54.62 = (9BC: 16)²+ Κυρ²
• 2981.16 = 81BC²: 256 + Κυρ²
• 2981,16 = 337 π.Χ.²: 256
• 337BC² = 763176.96
• Κυρ² = 2264.62
• VS = 47,59 (cm)

Απάντηση: το πλάτος του τριγώνου είναι 47,59 cm.

Πρόβλημα 5. Η διαγώνιος και η γωνία

Εμφανίζεται το ορθογώνιο του ABCD, η διαγώνιος του οποίου είναι 8 cm, και η γωνία είναι 30 μοίρες. Είναι απαραίτητο να βρείτε το πλάτος του ορθογωνίου.

Λύση: δεδομένου ότι η γωνία ABC είναι ευθεία, το τρίγωνο ABC είναι ορθογώνιο,

hypotenuse, και AB και BC είναι τα πόδια. Είναι γνωστό ότι ο καθετήρας, που βρίσκεται σε γωνία 30 μοιρών, είναι ίσος με το ήμισυ της υποτείνουσας. Αποδεικνύεται:

• BC = AC: 2 = 8: 2 = 4 (cm)

Απάντηση: το πλάτος του ορθογωνίου είναι 4 cm.

Όπως μπορείτε να δείτε, τα τυπικά καθήκοντα για την εύρεση του πλάτους ενός ορθογωνίου είναι αρκετά απλά. Το κύριο πράγμα είναι να γνωρίζουμε τους τύπους και τις ιδιότητες ενός ορθογωνίου και ορθογώνια τρίγωνα.

Αν θέλετε να βρείτε το μήκος ενός ορθογωνίου, διαβάστε το άρθρο - Ποιο είναι το μήκος του ορθογωνίου.