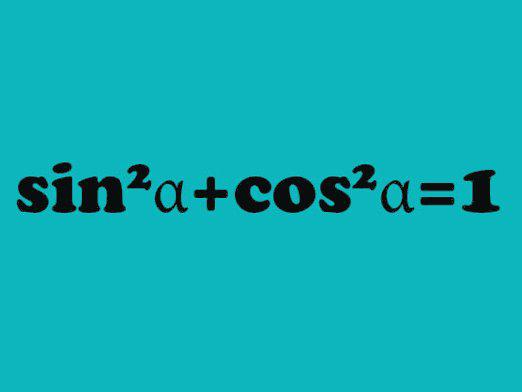Πώς να βρείτε το ημίτονο της γωνίας ενός τριγώνου;

Για να βρούμε το ημίτονο της γωνίας ενός ορθογώνιου τριγώνου, πρέπει να θυμηθούμε τι είναι ημιτονική εξ ορισμού. Και ο ορισμός είναι πολύ απλός: το ημίτονο της γωνίας είναι ίσο με το λόγο του αντίθετου ποδιού προς την υποτείνουσα.
Πώς να υπολογίσετε το sines
Εάν έχουμε ένα τρίγωνο ABC, για το οποίο A -μια δεξιά γωνία, τότε οι πλευρές AB και AC θα είναι τα πόδια, και η πλευρά BC - hypotenuse. Ως εκ τούτου, εξ ορισμού, το ημίτονο της γωνίας Β είναι ίσο με την αναλογία του σκέλους του AC με την υποτείνουσα: sinB = AC / BC, και το ημίτονο της άλλης γωνίας sinC = AB / BC.
Σε ένα ορθογώνιο τρίγωνο, οι λειτουργίες των γωνιώνείναι βολικό να υπολογίσετε: δεν χρειάζονται πρόσθετες κατασκευές. Αρκεί να γνωρίζουμε το μήκος των δεξιών πλευρών. Αλλά πιο συχνά μόνο ένα μέρος των απαραίτητων δεδομένων είναι γνωστό, το υπόλοιπο πρέπει να αναζητηθεί. Εξετάστε πώς να το κάνετε αυτό.
Ψάχνετε για ένα ημίτονο με δύο πόδια
Παίρνουμε το ίδιο τρίγωνο ABC με ορθή γωνία Α, στην οποία γνωρίζουμε τις διαστάσεις των ποδιών: AB = a, AC = c. Για να υπολογίσουμε το ημίτονο της γωνίας C, είναι απαραίτητο να διαιρέσουμε τον καθετήρα σε υποτείνουσα:
- sinC = AB / BC = a / BC (1).
Αλλά η hypotenuse θα πρέπει να εξεταστεί σύμφωνα με το Πυθαγόρειο θεώρημα:
- BC = √ (AB² + AC²) = √ (a² + b²). (2)
Παρέχουμε την εύρεση της υποτινούσης (2) στην έκφραση (1), παίρνουμε την απάντηση:
- sinC = a / √ (a2 + b2).
Ψάχνετε για ένα ημιτονοειδές στην υποτείνουσα και το γειτονικό πόδι
Τώρα, στο ίδιο τρίγωνο, πρέπει να βρούμε το ημίτονο της ίδιας γωνίας Γ, αλλά γνωρίζουμε την υποτείνουσα BC = b και την κάθοδο AC = c. Με τη βοήθεια του θεώρημα Pythagorean: AB² + AC² = BC² ψάχνουμε για το AB:
- AB = √ (b²-c²).
Τώρα αντικαταστήστε την διαπιστωμένη τιμή του ΑΒ στον τύπο για το ημίτονο:
- sinC = ΑΒ / β = √ (b2-c2) / b.
Υπολογισμός ολίσθησης στη μία πλευρά και αιχμηρή γωνία
Στο τρίγωνο ABC με ορθή γωνία Α, η γωνία Β = β είναι γνωστή, και η κάθαρση AC = c. Πρέπει να βρούμε το ημίτονο της γωνίας C.
Μέθοδος 1.
Το πιο απλό - αν θυμάστε ότι το άθροισμα όλων των γωνιών στο τρίγωνο είναι 180 °:
- Α + Β + C = 180 °.
- Η γωνία Α = 90 °, Β = β,
- C = 180 ° -90 ° - β = 90 ° - β.
- Ως εκ τούτου sinC = sin (90 ° - β).
Μέθοδος 2.
Αλλά μπορείτε να πάτε με τον άλλο τρόπο:
- Sinβ = AC / BC. Sinβ = c / BC. Από εδώ:
- BC = c / Sinβ.
Από το θεώρημα του Pythagoras AB2 + AC2 = BC2 βρίσκουμε την υποτείνουσα:
- AB = √ (BC²-AC²).
Αντικαθιστά τις γνωστές τιμές:
- AB = √ (s² / Sin²β-c²) = √с² (1 / Sin²β-1) = σ√ (1 / Sin²β-1).
Επομένως βρίσκουμε το ημίτονο της γωνίας C:
- sinC = AB / BC = c√ (1 / Sin²β-1) / s / Sinβ = Sinβ √ (1 / Sin²β-1)
Απάντηση:
- sinc = Sinβ √ (1 / Sin²β-1).