Σημάδια παραλληλισμού των ευθειών γραμμών

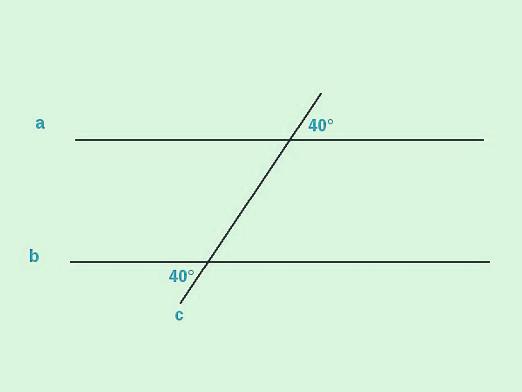
Ο παραλληλισμός των δύο γραμμών μπορεί να αποδειχθείη βάση του θεωρήματος, σύμφωνα με την οποία δύο κάθετες κάθετες προς μία ευθεία γραμμή θα είναι παράλληλες. Υπάρχουν ορισμένες ενδείξεις παραλληλισμού των γραμμών - υπάρχουν μόνο τρεις από αυτές και όλοι θα εξετάσουμε πιο συγκεκριμένα.

Το πρώτο σημάδι παραλληλισμού

Οι ευθείες γραμμές είναι παράλληλες, αν στη διασταύρωση της τρίτης ευθείας τους, οι σχηματισμένες εσωτερικές γωνίες που βρίσκονται στην αντίθετη κατεύθυνση θα είναι ίσες.

Ας υποθέσουμε, κατά τη διέλευση των γραμμών AB και CD της γραμμήςαπό τη γραμμή EF, σχηματίστηκαν οι γωνίες 11 και 12. Είναι ίσες, καθώς η ευθεία γραμμή EF περνά κάτω από μία κλίση σε σχέση με τις άλλες δύο ευθείες γραμμές. Στη διασταύρωση των γραμμών, βάζουμε τα σημεία Ki L - έχουμε αποκτήσει ένα τμήμα του secant EF. Βρίσκουμε τη μέση του και βάζουμε το σημείο O (Εικ. 189).

Στη γραμμή AB χαμηλώνουμε την κάθετο από το σημείο O. Το ονομάζουμε OM. Συνεχίστε την κάθετη έως ότου τέμνει το ευθεία CD. Ως αποτέλεσμα, η αρχική γραμμή AB είναι αυστηρά κάθετη προς MN, πράγμα που σημαίνει ότι το CD_ | _MN, αλλά αυτή η δήλωση απαιτεί απόδειξη. Ως αποτέλεσμα κατακόρυφων και διασταυρωμένων γραμμών έχουμε σχηματίσει δύο τρίγωνα. Ένας από αυτούς είναι δικός μου, ο δεύτερος είναι ΝΟΚ. Ας τις εξετάσουμε λεπτομερέστερα. σημάδια παραλληλισμού των γραμμών 7 τάξης

Αυτά τα τρίγωνα είναι ίσα επειδή, στοΣύμφωνα με τις συνθήκες του θεώρημα, / 1 = / 2, και σύμφωνα με την κατασκευή των τριγώνων, η πλευρά ΟΚ = πλευρά OL. Η γωνία MOL = / NOK, αφού είναι κάθετες γωνίες. Από αυτό προκύπτει ότι η πλευρική και οι δύο γωνίες που γειτονεύουν με αυτό ενός από τα τρίγωνα είναι αντίστοιχα ίσες με την πλευρά και τις δύο γωνίες που γειτνιάζουν με αυτό, το άλλο από τα τρίγωνα. Έτσι, το τρίγωνο MOL = triangleNOK, και ως εκ τούτου η γωνία LMO = η γωνία του KNO, αλλά γνωρίζουμε ότι η LMO είναι ευθεία, εξ ου και η αντίστοιχη γωνία KNO είναι επίσης μια ευθεία γραμμή. Δηλαδή, κατορθώσαμε να αποδείξουμε ότι στη γραμμή MN, τόσο η γραμμή ΑΒ, όσο και η ευθεία γραμμή CD είναι κάθετες. Δηλαδή, το AB και το CD σε σχέση με το άλλο είναι παράλληλα. Αυτό θέλαμε να αποδείξουμε. Εξετάστε τα υπόλοιπα σημάδια παράλληλων γραμμών (7η τάξη), τα οποία διαφέρουν από το πρώτο χαρακτηριστικό με τη μέθοδο απόδειξης.

Το δεύτερο σημάδι παραλληλισμού

Σύμφωνα με το δεύτερο σημάδι παραλληλισμού των ευθειών γραμμών,πρέπει να αποδείξουμε ότι οι γωνίες που λαμβάνονται κατά τη διασταύρωση των παράλληλων γραμμών AB και CD της γραμμής EF είναι ίσες. Έτσι, τα σημάδια παραλληλισμού των δύο ευθειών γραμμών, τόσο του πρώτου όσο και του δεύτερου, βασίζονται στην ισότητα των γωνιών που λαμβάνονται όταν τέμνονται με την τρίτη γραμμή. Υποθέτουμε ότι το / 3 = / 2, και η γωνία 1 = / 3, αφού είναι κατακόρυφο σε αυτό. Επομένως, το f2 θα είναι ίσο με την γωνία 1, αλλά θα πρέπει να ληφθεί υπόψη ότι τόσο η γωνία 1 όσο και η γωνία 2 είναι εσωτερικές, διασταυρούμενες γωνίες. Επομένως, μένει να εφαρμόσουμε τις γνώσεις μας, δηλαδή ότι δύο τμήματα θα είναι παράλληλα αν, στη διασταύρωσή τους, την τρίτη ευθεία, οι σχηματισμένες, αμοιβαία γειτονικές γωνίες είναι ίσες. Έτσι, διαπιστώσαμε ότι το AB || CD.

Καταφέραμε να αποδείξουμε ότι υπό την προϋπόθεση του παραλληλισμού δύο καθέτων προς μία ευθεία γραμμή, σύμφωνα με το αντίστοιχο θεώρημα, ο παραλληλισμός των γραμμών είναι προφανής.

Το τρίτο σημάδι παραλληλισμού

Υπάρχει επίσης ένα τρίτο σημάδι παραλληλισμού,που αποδεικνύεται μέσω ενός αθροίσματος μονόπλευρων εσωτερικών γωνιών. Μια τέτοια απόδειξη του παραλληλισμού των γραμμών μας επιτρέπει να καταλήξουμε στο συμπέρασμα ότι δύο ευθείες γραμμές θα είναι παράλληλες εάν, στη διασταύρωση της τρίτης γραμμής τους, το άθροισμα των λαμβανόμενων μονόπλευρων εσωτερικών γωνιών είναι ίσο με 2d. Βλ. Σχήμα 192.