Σημάδια ομοιότητας των τριγώνων
Σημάδια ομοιότητας δύο τριγώνων είναι τέτοια γεωμετρικά χαρακτηριστικά που μας επιτρέπουν να διαπιστώσουμε ότι δύο συγκεκριμένα τρίγωνα είναι παρόμοια μεταξύ τους, χωρίς να λαμβάνονται υπόψη όλα τα στοιχεία.
Θεώρημα 1
Το πρώτο σημάδι της ομοιότητας δύο τριγώνων
Τα τρίγωνα είναι παρόμοια εάν τουλάχιστον δύο γωνίες σε ένα τρίγωνο είναι αντίστοιχα ίσες με δύο γωνίες σε ένα άλλο τρίγωνο.
Απόδειξη.
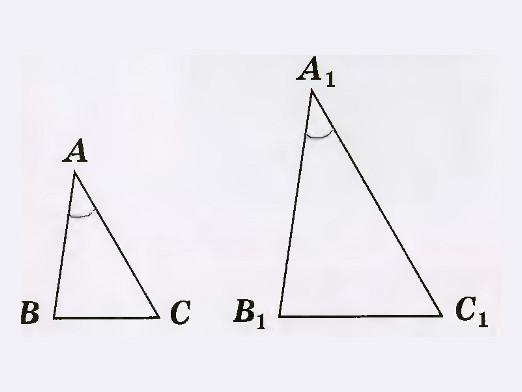
Εάν δίνονται δύο τρίγωνα: ABC και A1B1C1, όπου ∠Α = ∠A1, και ∠B = ∠B1. Τότε φαίνεται ότι το ∠C και το ∠C1 είναι επίσης ίσες. Ας αποδείξουμε την ομοιότητα των △ ABC και △ A1B1C1.
Εάν αναβάλλουμε από την πλευρά της VA ένα τμήμα BA2, το οποίοτμήμα θα είναι ίση με A1B1, και στη συνέχεια, σχεδιάστε μια ευθεία γραμμή από το σημείο Α2 η οποία είναι παράλληλη με τη γραμμή AC. Στη συνέχεια, αυτή η γραμμή θα διακόψει το τμήμα BC στο σημείο, το οποίο ονομάζουμε C2. Έτσι, τρίγωνα και A2VS2 A1V1S1 είναι: Α2Β = A1B1 με κατασκευή ∠V1 = ∠V σχετικά με την κατάσταση και ∠A2 = ∠A1 ως ∠A = ∠A1 σχετικά με την κατάσταση και ∠A2 = ∠A με τις αντίστοιχες γωνίες. Σύμφωνα με Λήμμα 1 της ομοιότητας τριγώνων (μία γραμμή η οποία είναι παράλληλη προς τη μία πλευρά του τριγώνου και τέμνει τις άλλες δύο πλευρές του, αποκόπτει το τρίγωνο, το οποίο είναι παρόμοιο με αυτό), έχουμε: △ ABC ~ △ A2BC2, έτσι, △ A1B1C1 ~ △ ABC. Ως εκ τούτου, το θεώρημα αποδεικνύεται. Τα θεωρήματα 2 και 3 αποδεικνύονται από ένα παρόμοιο σχήμα.
Θεώρημα 2
Το δεύτερο σημείο της ομοιότητας των τριγώνων.
Τα τρίγωνα θεωρούνται παρόμοια αν δύο από ταοι πλευρές ενός τριγώνου θα είναι ανάλογες προς τις δύο πλευρές του δεύτερου τριγώνου, αντίστοιχα. Επίσης, πρέπει να τηρείται η προϋπόθεση της ισότητας των γωνιών μεταξύ αυτών των μερών.
Θεώρημα 3
Το τρίτο σημείο της ομοιότητας των τριγώνων.
Τα τρίγωνα θεωρούνται παρόμοιες, αν η παρακάτω προϋπόθεση της αναλογικότητας στις τρεις πλευρές της από αυτές τις τρεις πλευρές του δεύτερου.
Απόρροια 1 του θεωρήματος 1. Αν εξετάσουμε τέτοια τρίγωνα, τότε οι παρόμοιες πλευρές τους θα είναι ανάλογες με τα ύψη που θα παραλειφθούν σε παρόμοιες πλευρές.
Σημάδια της ομοιότητας των ορθογωνίων τριγώνων
- τα ορθογώνια τρίγωνα θεωρούνται παρόμοια αν ο κώδωνας και η υποτείνουσα του ενός είναι ανάλογοι με το πόδι και την υποτείνουσα του δεύτερου τριγώνου.
- τα ορθογώνια τρίγωνα θεωρούνται παρόμοια αν η οξεία γωνία ενός από αυτά είναι ίση με την οξεία γωνία του δεύτερου τριγώνου.
Σημάδια ομοιότητας τριγώνων σε παραδείγματα
Παράδειγμα 1
Είναι απαραίτητο να βρεθεί το μήκος του τμήματος KP, εάν είναι γνωστό,ότι στο τρίγωνο ABC, το μήκος της πλευράς AC είναι δέκα, και στην πλευρά AB υπάρχει ένα ορισμένο σημείο K, αλλά AK = 2, BK = 3. Μια ευθεία γραμμή τραβιέται από το σημείο Κ, το οποίο είναι παράλληλο με το AC. Το σημείο P βρίσκεται στη διασταύρωση του με την πλευρά BC. Αυτή είναι η κατάσταση όταν χρησιμοποιούνται σημεία ομοιότητας τριγώνων. Ένα μάθημα με παρόμοιο πρόβλημα βρίσκεται πάντοτε σε κάθε σχολείο. Έτσι, εάν υπάρχει μια ευθεία γραμμή στο τρίγωνο, που είναι παράλληλη προς τη μία πλευρά, τότε σχηματίζεται ένα τρίγωνο που είναι παρόμοιο με αυτό. Το τρίγωνο CBS είναι παρόμοιο με το τρίγωνο ABC. Αποδεικνύοντας αυτό, παρατηρούμε ότι η γωνία του SRS είναι ίση με τη γωνία του BAC. Λαμβάνοντας υπόψη ότι αυτές είναι οι αντίστοιχες γωνίες, οι οποίες βρίσκονται με παράλληλη RS και AC και ακραίες AK. Επιπλέον, η γωνία Β είναι μια κοινή γωνία, και κατά συνέπεια, οι τρίτες γωνίες είναι ίσες, η γωνία του BPM και του BCA. Έτσι, σύμφωνα με το θεώρημα για το πρώτο κριτήριο για την ομοιότητα των τριγώνων, το ∠ ABC είναι παρόμοιο με το ∠CR. Από αυτό προκύπτει ότι το KP / AC, οι πλευρές που βρίσκονται επάνω στο ∠B, είναι ίσες με την πλευρά VK / Va, τις πλευρές που βρίσκονται ενάντια στα ίσα ∠P και ∠C. Επομένως, βρίσκουμε το τμήμα BA προσθέτοντας BK και AK. Υπολογίζουμε τα δεδομένα, τα οποία λαμβάνουμε: KR / 10 = 3/5, δηλαδή, KP = 6
Παράδειγμα 2
Αφήστε στα τρίγωνα ABC και A1B1C1, ∠B = ∠B1. Τα μέρη AB, BC στο τρίγωνο ABC είναι 2,5 φορές μεγαλύτερα από τις πλευρές A1B1, B1C1, που είναι στο τρίγωνο A1B1C1. Είναι απαραίτητο να βρεθούν AC και A1C1, υπό την προϋπόθεση ότι το ποσό τους είναι 4,2 μ. Λύση. Με την κατάσταση του προβλήματος, γράφουμε:
- ∠B = ∠B1;
- AB / A1B1 = BC / B1C1 = 2.5 Συνεπώς, ΔΔ ABC ~ Δ A1B1C1. Με το δεύτερο σημείο της ομοιότητας των τριγώνων.
- AC + A1C1 = 4,2 m. Από την ομοιότητα αυτών των τριγώνων λαμβάνουμε το αποτέλεσμα AC / A1C1 = 2.5, ή AC = 2.5xA1C1.Αν AC = 2.5 x A1C1 τότε AC + A1C1 = 2.5 x A1C1 + A1C1 = 4.2, συνεπώς AC = 3 (m), A1C1 = 1,2 (m).
Παράδειγμα 3
Είναι απαραίτητο να μάθουμε αν τα τρίγωνα είναι παρόμοιαA1B1C1 και ABC εάν cm, BC = 5 cm, ΑΒ = 3, AC = 7 cm, B1C1 = 7,5 cm, A1B1 = 4,5 cm, A1C1 = 10,5 cm- Η λύση. BC / B1C1 = 5 / 7,5 = 1 / 1,5 ΑΒ / Α1Β1 = 3 / 4,5 = 1 / 1,5 AC / A1C1 = 7 / 10,5 = 1 / 1,5
Ως εκ τούτου, από το τρίτο σημείο, τα τρίγωνα είναι παρόμοια.