Σημάδια ισότητας τριγώνων

Όλοι γνωρίζουν ότι δύο τμήματα θα είναι ίσα αντα μήκη τους συμπίπτουν. Ή κύκλοι μπορούν να θεωρηθούν ίσοι εάν οι ακτίνες τους είναι ίσες. Και ποια είναι τα σημάδια της ισότητας των τριγώνων; 7η τάξη της δευτεροβάθμιας εκπαίδευσης: στο μάθημα της γεωμετρίας, οι μαθητές μαθαίνουν ότι, αποδεικνύεται, υπάρχουν στοιχεία για τα οποία η ισότητα μπορεί να θεωρηθεί ίση με τα τρίγωνα που τα περιέχουν. Είναι πολύ βολικό να χρησιμοποιείται για την επίλυση προβλημάτων.

Το πρώτο σημάδι της ισότητας των τριγώνων

Η τήρηση της κατάστασης της αντίστοιχης ισότηταςδύο πλευρές και μία γωνία μεταξύ τους η οποία περικλείεται σε ένα τρίγωνο και δύο πλευρές της γωνίας που περικλείεται μεταξύ τους στο άλλο τρίγωνο, προτείνει ότι αυτά τα τρίγωνα είναι ίσα.

Απόδειξη.

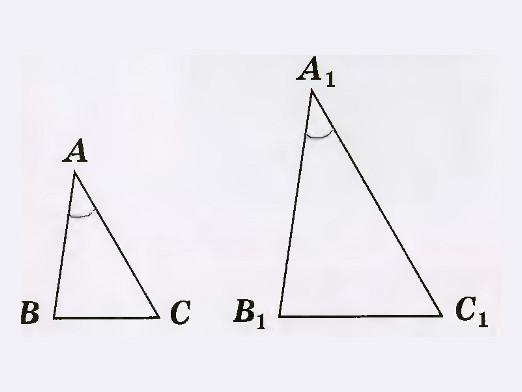
Αν σκεφτούμε △ ABC και △ A1B1C1, όπου οι πλευρές AB = A1B1, BC = B1C1,

και ∠ABC ισούται με ∠ A1B1C1,

τότε △ A1B1C1 μπορεί να τοποθετηθεί πάνω από το △ ABC με τέτοιο τρόπο ώστε ∠ A1B1C1 να συμπίπτει με το ∠ABC. Στην περίπτωση αυτή, τα τρίγωνα συμπίπτουν εντελώς, επειδή όλες οι κορυφές τους συμπίπτουν.

(Εάν είναι απαραίτητο, το τρίγωνο A1B1C1 μπορεί να αντικατασταθεί από ένα ίσο "ανεστραμμένο" τρίγωνο, δηλαδή ένα τρίγωνο συμμετρικό με το A1B1C1.)

Το δεύτερο σημείο της ισότητας των τριγώνων

Υπό την προϋπόθεση ότι μία πλευρά και δύο γωνίες που είναιείναι πλησίον αυτής, αντίστοιχα πλευρά ένα τρίγωνο και δύο γωνίες οι οποίες είναι πλησίον αυτής στο άλλο τρίγωνο, αυτές οι τρίγωνα θεωρούνται ίσες.

Απόδειξη.

Εάν σε △ ABC και △ A 1 B 1 C 1 διατηρούνται οι ακόλουθες ισοτιμίες

ΑΒ = A1B1,

∠BAC = ∠B1A1C1,

∠ABC = ∠A1B1C1.

Τοποθετούμε τα τρίγωνα A1B1C1 και ABC μεταξύ τουςέτσι ώστε να συμπίπτουν οι ίσες πλευρές ΑΒ και Α1Β1 και οι γωνίες που τα συνοδεύουν. Όπως και στο προηγούμενο παράδειγμα, εάν είναι απαραίτητο, το τρίγωνο A1B1C1 μπορεί να "γυριστεί και να επιστρέψει". Τα τρίγωνα συμπίπτουν και επομένως μπορούν να θεωρηθούν ίσα.

Το τρίτο σημείο της ισότητας των τριγώνων

Υπό την προϋπόθεση ότι οι τρεις πλευρές ενός τριγώνου είναι ίσες με τις τρεις πλευρές ενός άλλου τριγώνου, τότε τα τρίγωνα θεωρούνται ίσες. Απόδειξη.

Ας υποθέσουμε ότι για το △ ABC και △ A1B1C1 οι ισοτιμίεςA1B1 B1C1 = ΑΒ = BC = CA S1A1 Μετακίνηση A1V1S1 τρίγωνο έτσι ώστε η πλευρά A1B1 sovpdet με πλευρικές ΑΒ, και οι κορυφές Β1 και Β, Α1 και Α, συμπίπτουν. Θεωρήστε έναν κύκλο με το κέντρο του σε Α και μία ακτίνα AC, και ένα δεύτερο κύκλο με κέντρο Β και ακτίνα BC. Αυτές οι κύκλοι τέμνονται σε δύο συμμετρικά σημεία σε σχέση με το τμήμα ΑΒ: σημείο C και το σημείο C2. Ως εκ τούτου, C1 μετά A1B1C1 μεταφορά τρίγωνο ή θα πρέπει να συμπίπτει με το σημεία C, ή C2. Είτε έτσι είτε αλλιώς, αυτό θα σημαίνει ισότητα △ ABC = △ A1B1C1, δεδομένου ότι τα τρίγωνα △ ABC = △ ABC2 ίσα (δεδομένου ότι τα τρίγωνα είναι συμμετρικές σε σχέση με το τμήμα ΑΒ.)

Σημάδια ισότητας τριγώνων ορθογωνίου

Σε ορθογώνια τρίγωνα, η γωνία μεταξύ των ποδιών είναι μια ευθεία γραμμή, επομένως σε οποιοδήποτε ορθογώνιο τρίγωνο υπάρχουν ήδη ίσες γωνίες. Ως εκ τούτου, ισχύουν οι ακόλουθες παρατηρήσεις.

• Τα ορθογώνια τρίγωνα είναι ίσα αν τα πόδια ενός από αυτά είναι ίσα με τα πόδια του άλλου.
• Τα ορθογώνια τρίγωνα είναι ίσα, αν πληρούται η προϋπόθεση της αντίστοιχης ισότητας της υποτείνουσας και ενός από τα πόδια στα τρίγωνα αυτά.

Εάν αφαιρέσουμε από το δεύτερο κριτήριο, το οποίο μιλάει για την ισότητα των τριγώνων, η προϋπόθεση για την ευθεία γωνία δίπλα στο πόδι (καθώς οι ορθές γωνίες στα τρίγωνα είναι ίσες), έχουμε τα εξής:

• αυτά τα τρίγωνα είναι ίσα, υπό την προϋπόθεση ότι το παλάτικαι επίσης η οξεία γωνία παρακείμενη σε αυτό σε ένα ορθογώνιο τρίγωνο, αντίστοιχα, είναι ίσες με το πόδι και την οξεία γωνία, σε ένα άλλο ορθογώνιο τρίγωνο.

Είναι γνωστό ότι το άθροισμα των εσωτερικών γωνιών ενός τριγώνουείναι πάντα 180 °, και μία από τις γωνίες ενός δεξιού τριγώνου είναι μια ευθεία γραμμή. Επομένως, αν σε δύο ορθογώνια τρίγωνα οι οριζόντιες γωνίες είναι ίσες, τότε οι υπόλοιπες γωνίες είναι ίσες. Για κανονικά, μη ορθογώνια τρίγωνα, για να προσδιοριστεί η ισότητα των μορφών, αρκεί να γνωρίζουμε ότι η μια πλευρά και οι δύο γωνίες που αντιστοιχούν σε αυτήν είναι ίσες, αντίστοιχα. Σε ένα ορθογώνιο τρίγωνο, μόνο μια οξεία γωνία και hypotenuse μπορεί να θεωρηθεί ότι καθορίζει την ισότητα των μορφών.

• Τα ορθογώνια τρίγωνα θα είναι ίσα υπό την προϋπόθεση ότι η οξεία γωνία και η υπόταση ενός από αυτά είναι ίσα με την οξεία γωνία και την υποτείνουσα στην άλλη.

Καταπληκτική επιστήμη - γεωμετρία! Τα σημάδια της ισότητας των τριγώνων μπορούν να είναι χρήσιμα όχι μόνο για σχολικά εγχειρίδια αλλά και για την επίλυση καθημερινών προβλημάτων που οι ενήλικες επιλύουν στην καθημερινή ζωή.