Πώς να βρείτε το μήκος της τρίτης πλευράς του τριγώνου;
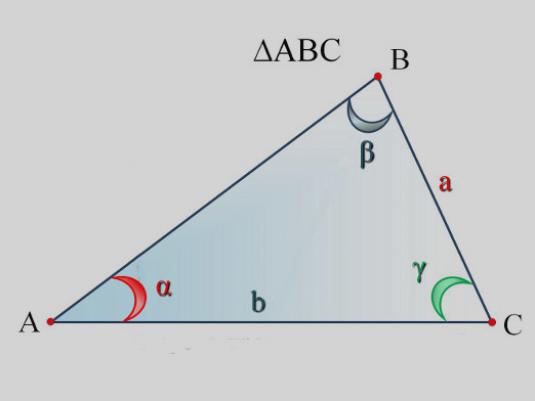
Το πρόβλημα της επίλυσης τριγώνων (αυτό είναι το όνομα τέτοιων προβλημάτων) χειρίζεται ένα ειδικό τμήμα της γεωμετρίας - τριγωνομετρίας.
Το μήκος των δύο πλευρών του τριγώνου
Βρείτε το μήκος της τρίτης πλευράς του τριγώνουορθογώνιο πρότεινε τον αρχαίο μαθηματικό Πυθαγόρα γνωστό σε όλους. Η βάση είναι ένα ορθογώνιο τρίγωνο, δηλαδή, ένα από τα οποία οι γωνίες είναι ίσες με 90 μοίρες. Οι γειτονικές πλευρές αυτής της γωνίας αναφέρονται πάντοτε ως τα πόδια, αντίστοιχα, η τρίτη, η μεγαλύτερη πλευρά, ονομάζεται "υποτείνουσα". Το θεώρημα του Πυθαγόρα έχει ως εξής: "Το τετράγωνο του μήκους της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των μηκών των ποδιών".
Για την επίλυση ενός τέτοιου προβλήματος, η αξία του μήκους ενόςΟρίζουμε το πόδι ως X (X) και το άλλο Y (ζεύγος), το μήκος της υποτείνουσας μπορεί να χαρακτηριστεί ως Z (z). Τώρα ας γράψουμε τον τύπο για τον υπολογισμό του μήκους της υποτείνουσας: Ζ τετράγωνο = Χ τετράγωνο + Y τετράγωνο. Προχωρώντας από μια τέτοια φόρμουλα, παίρνουμε τελικά την τιμή του τετραγώνου του μήκους της υποτείνουσας. Επομένως, για να ληφθεί η τιμή του μήκους της υποτείνουσας, είναι ακόμα αναγκαίο να εξαχθεί η τετραγωνική ρίζα του προκύπτοντος άθρου των μηκών των ποδιών.
Προηγουμένως, θεωρήσαμε την ιδανική επιλογή, ότανείναι απαραίτητο να προσδιοριστεί το μήκος της υποτείνωσης. Εάν ένα πρόβλημα είναι άγνωστο μήκος ενός από τα σκέλη, τότε, που βασίζονται στο παρόν θεώρημα, μπορούμε να αντλήσουμε έναν τύπο παραγώγου. Το τετράγωνο του μήκους ενός από τα σκέλη είναι ίση με μια τιμή που λαμβάνεται με αφαίρεση της τετράγωνο του μήκους του άλλου σκέλους της πλατείας του μήκους της υποτείνουσας: Χ = Ζ τετράγωνο τετράγωνο - Y τετράγωνο. Λοιπόν, η τελευταία ενέργεια απαιτείται για να εξαγάγετε την τετραγωνική ρίζα της τιμής που λαμβάνεται.
Για παράδειγμα, λάβετε τις απλές τιμές του μήκουςκυψελίδες: 2 και 3 εκατοστά. Με απλές μαθηματικές πράξεις, παίρνουμε το τετράγωνο Z = 4 + 9 = 13. Αυτό σημαίνει ότι το Z είναι περίπου 3,6 εκατοστά. Αν αποκλείσουμε την τετραγωνισμό των τιμών, αποδεικνύεται ότι Z = 2 + 3 = 5 εκατοστά, πράγμα που δεν αντιστοιχεί στην αλήθεια.
Με το μήκος των δύο πλευρών και από την τιμή της γωνίας μεταξύ τους
Είναι δυνατό να βρεθεί το μήκος της τρίτης πλευράς του τριγώνου,χρησιμοποιώντας το θεώρημα συνημιτόνου. Αυτό γεωμετρικό θεώρημα είναι ως εξής: ένα τετράγωνο μια πλευρά του τριγώνου είναι ίση με την τιμή που λαμβάνεται με αφαίρεση δύο φορές το μήκος του προϊόντος γνωστές πλευρές και συνημίτονο της γωνίας το οποίο είναι διατεταγμένο μεταξύ τους, του αθροίσματος των τετραγώνων των γνωστών πλευρών μήκους.
Σε μαθηματική μορφή ένας τέτοιος τύπος μοιάζειως εξής: τετράγωνο Ζ = Χ2 + Υ2-2 * Χ * Υ * cosC. Εδώ, τα Χ, Υ, Ζ δηλώνουν το μήκος όλων των πλευρών του τριγώνου και το C είναι η τιμή σε μοίρες της γωνίας που βρίσκεται μεταξύ των γνωστών πλευρών.
Για παράδειγμα, χρησιμοποιούμε ένα τρίγωνο, γνωστότων οποίων οι πλευρές είναι ίσες με 2 και 4 εκατοστά, και η γωνία μεταξύ τους είναι 60 μοίρες. Χρησιμοποιούμε τον παραπάνω τύπο και παίρνουμε: Z τετράγωνο = 4 + 16-2 * 2 * 4 * cos60 = 20-8 = 12. Το μήκος της άγνωστης πλευράς είναι 3,46 εκατοστά.