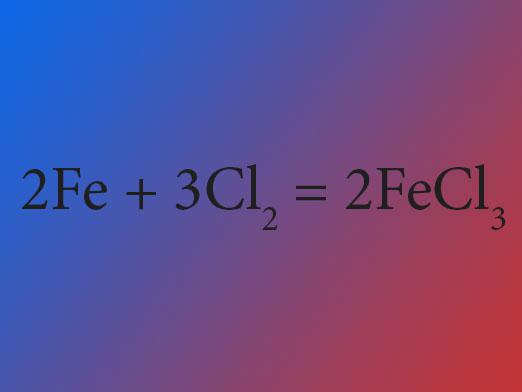Τι είναι παράγωγο;

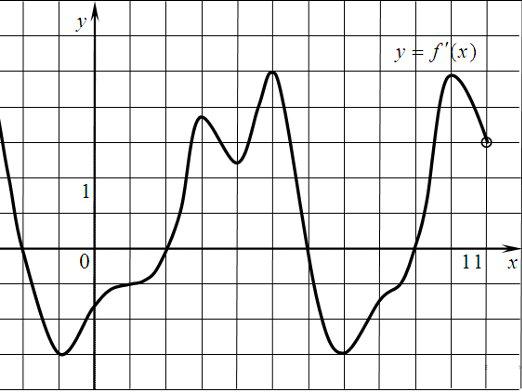
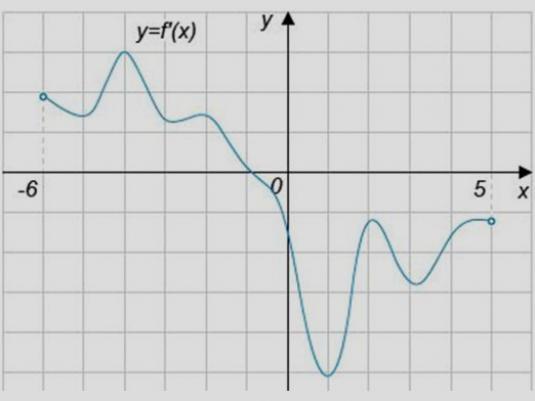
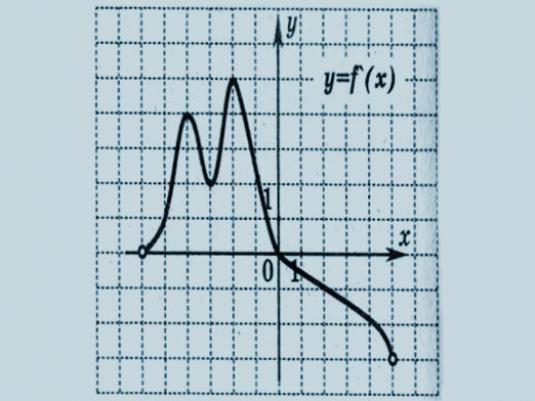
Μια παράγωγη συνάρτηση είναι ένα βασικό στοιχείο στοδιαφορικός υπολογισμός. Αυτό το στοιχείο είναι ένα οριστικό αποτέλεσμα της εφαρμογής ορισμένης λειτουργίας διαφοροποίησης σε σχέση με την αρχική λειτουργία.

Ορισμός του παραγώγου

Για να κατανοήσουμε τι είναι ένα παράγωγο,είναι απαραίτητο να γνωρίζουμε ότι το όνομα μιας συνάρτησης συμβαίνει απευθείας από τη λέξη "παράγεται", δηλαδή, σχηματίζεται από ένα άλλο οποιασδήποτε αξίας. Σε αυτή τη διαδικασία, η διαδικασία προσδιορισμού του παραγώγου μιας συγκεκριμένης συνάρτησης έχει το όνομα - "διαφοροποίηση".

Η πιο κοινή μέθοδος παρουσίασης καιΟρισμοί, χρησιμοποιώντας τη θεωρία των ορίων, παρά το γεγονός ότι εμφανίστηκε πολύ αργότερα από τα διαφορικά calculi. Με τον ορισμό αυτής της θεωρίας, το παράγωγο είναι το όριο σε σχέση με την αύξηση των λειτουργιών με την αύξηση του επιχειρήματος, εάν υπάρχει ένα τέτοιο όριο και με την προϋπόθεση ότι αυτό το επιχείρημα τείνει σε μηδενική τιμή.

Είναι γενικά αποδεκτό ότι, για πρώτη φορά, ο όρος και ο όρος "παράγωγο" χρησιμοποιήθηκαν στα έργα του από έναν γνωστό ρωσικό μαθηματικό με το όνομα VI Viskovatov.

Το παρακάτω μικρό παράδειγμα θα σας βοηθήσει να καταλάβετε τι είναι ένα παράγωγο.

1. Για να βρούμε το παράγωγο της συνάρτησης f στο σημείο x, πρέπει να καθορίσουμε τις τιμές αυτής της συνάρτησης απευθείας στο σημείο x, αλλά και στο σημείο x + Δx. Και Δx είναι οι αυξήσεις του argument x.
2. Βρείτε την αύξηση για τη συνάρτηση y που αντιστοιχεί σε f (x + Δx) - f (x).
3. Γράψτε το παράγωγο με τη βοήθεια του ορίου του λόγου f '= lim (f (x + Δx) - f (x)) / Δx, υπολογίστε για Δx → 0.

Συνήθως το παράγωγο συμβολίζεται με την απόστροφοΆμεσα πάνω από μια διαφοροποιήσιμη λειτουργία. Ο χαρακτηρισμός ως ενιαίο απόστροφο δηλώνει το πρώτο παράγωγο, με τη μορφή δύο - το δεύτερο. Το παράγωγο της υψηλότερης τάξης δίνεται συνήθως από το αντίστοιχο ψηφίο, για παράδειγμα f ^ (n) - που σημαίνει το παράγωγο της n-ου τάξης, όπου το γράμμα "n" είναι ένας ακέραιος που; 0. Το παράγωγο μηδενικής τάξης είναι η ίδια η διαφοροποιημένη συνάρτηση.

Προκειμένου να διευκολυνθεί η διαφοροποίηση των περίπλοκων λειτουργιών, αναπτύχθηκαν και εγκρίθηκαν ορισμένοι κανόνες για τη διαφοροποίηση των λειτουργιών:

• C '= 0, όπου C είναι η σταθερή ονομασία.
• το χ 'είναι 1.
• (f + g) 'ισούται με f' + g '.
• (C * f) 'ισούται με C * f' και ούτω καθεξής.
• Για Ν-φορές διαφοροποίηση, είναι πιο βολικό να εφαρμοστεί ο τύπος Leibniz στη μορφή: (f * g)^(η) = Σ C (n)^k* f^(n-k)* g^να, όπου C (n)^να - προσδιορισμός διωνυμικών συντελεστών.

Παραγώγων και Γεωμετρίας

Η γεωμετρική ερμηνεία του παραγώγου είναιτο ότι εάν η συνάρτηση f έχει ένα παράγωγο του τελικού σημείου x, η αξία του παραγώγου θα είναι ίση με την εφαπτομένη της γωνίας κλίσης του ενός εφαπτομένη στην συνάρτηση f σε αυτό το σημείο.